[8] NP and Computational Intractability
在本章節之前,我們發展了許多方法來有效率地解決問題,但還沒嘗試將不可有效率解決的問題量化或描述。嘗試用polynomial-time代表有效率且實務上可被解決,是一個好用的表示方式,因為這使得我們可以在數學上證明有些問題 不可被polynomial-time解決,也就是沒效率的。有些極度困難的問題,甚至無法證明其不存在Polynomial-time的演算法。
對於這樣難以描述的灰色地帶,近年來有一項大的進步,被證明以下論點:只要他們當中任一個存在polynomial-time Algorithm,就暗示全部都存在polynomial-time Algorithm。這些稱為NP-complete problems。儘管這些問題非常複雜使得我們仍難以解決,這項論點依舊說明一項極有力的事實:這些開放式的問題是 單一開放問題,是一種單一時間複雜度的問題,而我們尚無法解決。
從務實方面來看,NP-completeness 基本上代表:在實務目的上去計算處理非常困難,因此我們無法解決他。發現一問題是NP-complete problem代表我們可以停止去為這一問題搜尋有效率的演算法。
在這裡我們將現階段學習到全世界問題中的一小部分進行分類。
Complexity Classes
問題的分類,同一類有相同的complexity。
The class P : 能被Polynomial-time Algorithm解決的問題(但不一定真的寫的出來)。
The class NP(Non-deterministic Polynomial):可以在Polynomial-time 確認答案的問題,例如:得到Hamiltonian problem的答案可以直接去檢查是否真的是一筆畫連完所有點。
注意!
- NP不是Non - Polynomial或是Exponential。
- deterministic 指的是沒有固定步驟的。
- 全世界問題不是只有P和NP兩種,多的是更多更難的問題種類,這裡不探討。
The class NP-complete(NPC):NPC是NP裡面最難的問題。
Decision and Optimization Problems
再幫問題做難度分類之前,我們先大略將問題切為兩類:
- Optimization:找到合法的配置,使得cost最大或最小。
- MST:給一圖G,找到最小成本的延展樹,成本是多少?。
- TSP:給定complete graph(任兩點間相連),有點和邊(點間距離),找到經過每一點恰好一次的最短路徑,成本是多少?。
- Decision:回答YES/NO的問題。
- MST:給一圖G和上界K,是否存在成本最多為k的MST?
- TSP:給定complete graph(任兩點間相連),有點和邊(點間距離)、參數B,是否存在總距離為B的TSP最短路徑。
通常Optimization的難度會 ≧ Decision,以下會著重在Decision。
Intro some hard problems
Traveling man problem
給定一Complete Graph(任兩點間相連),且邊上有cost,找出經過各點恰一次且會回到原點的路徑。
Hamiltonian problem
給定任意undirected graph,各邊沒有weight,找出經過各點一次且回到原點的路徑。
(小時候可能玩過的一筆畫遊戲)
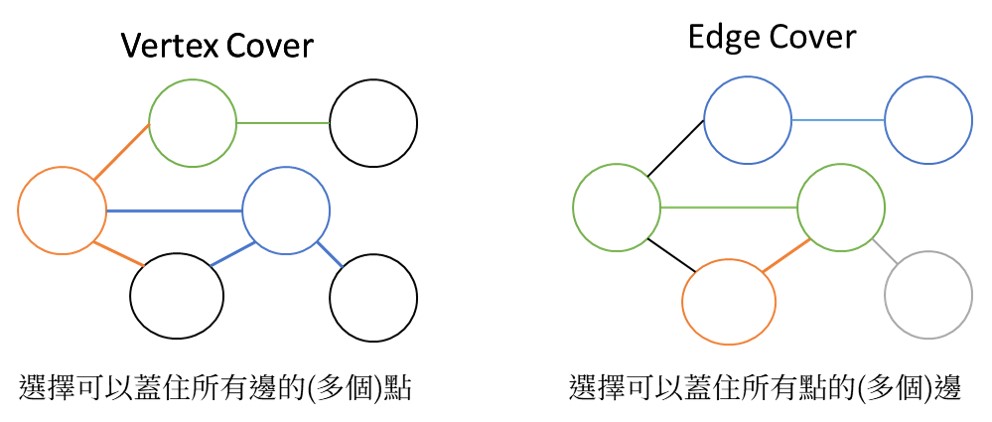
Vertex / Edge Cover
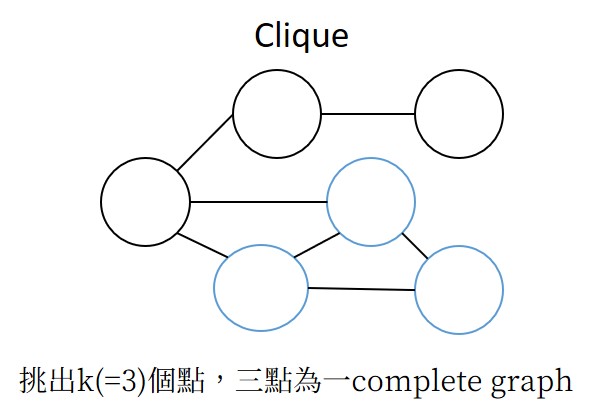
Clique
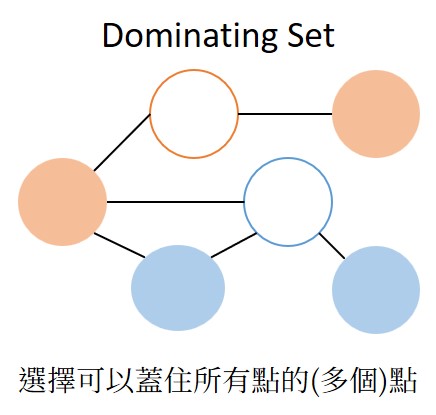
Dominating Set
Polynomial-Time Reduction
用Reduction的方式區分問題A的難度,已知問題B
白話一點,以Network flow(B)解決Bipartite Matching(A)這件事說明。如下圖,假設Bipartite Matching問題的難度未知,但是我們發現經過對輸入輸出作簡易改動,可以向右邊一樣用我們已知尋找Max Flow的演算法如Ford-Fulkerson完成。那麼我們就可以說Network flow較Bipartite Matching容易,若此時以證明Network flow是某一類問題中最難的(例如NPC),而剛剛又說Bipartite Matching又比他更難,所以兩者難度應是相等的,如此一來就證明了Bipartite Matching也屬於某類問題當中最難的。
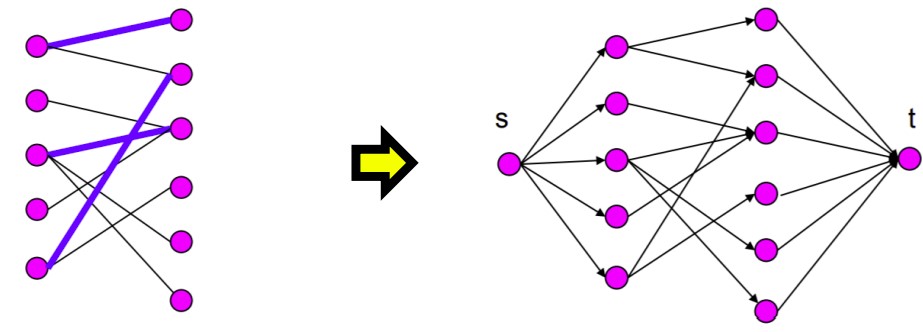
Notation:B≤pA(B reduces to A):B較A容易。
- A的演算法被視為一black box。
- 花費polynomial time的時間去改裝問題A。
Purpose
定義問題的難度。達到下面幾項目的:
Design Algorithm
用已知的演算法作改裝去解決未知的問題。
Establish Intractability
若X≤pY且X不可被polynomial time解決,那麼Y不可被polynomial time解決。開玩笑說,你可以拿來證明這問題根本沒法解決不要再逼我了。
Establish equivalence
X≤pY 且 Y≤pX,X = pY。
Prove NP-Completeness
A decision problem L is NP-complete(NPC) if L ∈ NP, and L′≤p for an L′∈ NPC。
有點循環論證的感覺,但是假設我們已經有第一個NPC問題A,那麼問題B又比A難,但是又說A是最難的,所以A和B一樣難,都是最難的(NPC)。
註:NP-hard直覺一點可以想成optimization版的NP-complete。
5 steps for proving that L is NP-complete
在已有第一個NP-complete 問題可使用的狀況下。
- 證明 L∈ NP。(L的解是否可在polynomial time驗證)
- 選一個已知的 NP-complete problem L'
- 用reduction f將所有L'的物件轉換為L的物件
- 證明f是polynomial-time的轉換
- 證明x∈L' iff f(x) ′∈L for all x ′∈{0,1} (0,1 means YES/NO (decision problem))
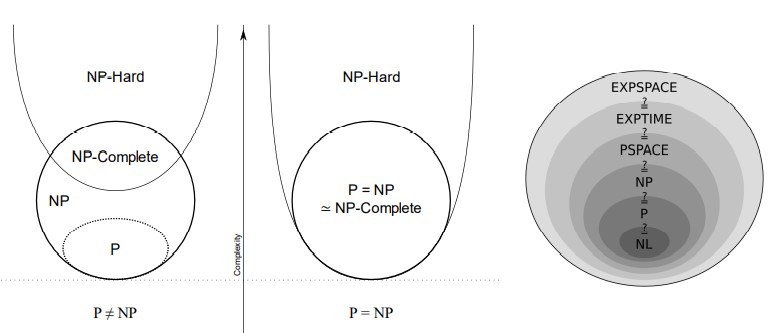
P and NP
目前P和NP的問題仍未被解決,因此就出現下面幾種可能的情況,唯一可以確認的一件事是「P與NP並非所有問題的集合」,因為我們定義了P是可以被多項式解決;而NP是可以被多項式驗證的。
The First Proved NPC:Circuit Satisfiability
上面說的Reduction及五步驟的證明有一項重要的前提,就是必須要有第一個NPC的問題被證明才行,而最早的NPC問題就是由Cook-Levin提出的SAT(Find a satisfying assignment),是一種電路問題。這裡不討論他是如 和證明的,但這項證明為這渾沌的問題世界帶來一道曙光!
CNF-CIRCUIT-SAT
Conjunctive Normal Form(CNF)指的是一種 propositional(Boolean) formula F ,F = C1∧ C2 ∧ C3∧...∧Cn,當中的每一個Ci稱為clause。而Ci = l1∨ l2 ∨ l3...∨ lk,當中的每個lj稱為literal ,literal是一個單純的布林值或是其加上not(~,¬,!)。注意!literal指的並非只能是 一個 變數!!
Implement Reduction
CNF-SAT ≤p 3-CNF-SAT
SAT跟CNF-SAT這裡不證明其為NP-complete而是直接作為使用(假設已知),來示範如何證明3-CNF-SAT為NP-complete,並可作為接下來證明其他問題的工具。(3-CNF-SAT指的是每個clause有三個literal的CNF-SAT)
根據上面五步驟主要要做的是:
- 已知3-CNF-SAT是NP
- 用CNF-SAT作reduction,使得CNF-SAT ≤p 3-CNF-SAT,但我們又已知CNF-SAT是NP-complete,代表 3-CNF-SAT至少跟 CNF-SAT一樣難,也就是說3-CNF-SAT是NP-complete。
改裝CNF-SAT
每次只針對一個clause C就好,若
C恰為三個literal,不用更動
C < 三個literal,複製到滿三個
例如 C 是(x ∨ ¬y)複製成(x ∨ x ∨ ¬y)
C > 三個literal,加入新變數λ1,λ2,...並且替代掉原先的C
新變數λ的規則
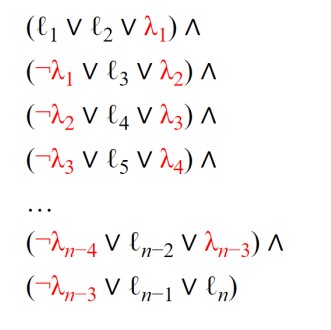
範例 : (x ∨ ¬y ∨ z ∨ u ∨ ¬v)
讓兩問題的Instance互相對映
CNF-SAT → 3-CNF-SAT
假設CNF是satisfiable,也就是最後會輸出true,代表每個clause都會是true,也代表每個cluase內至少有一個literal是true。
挑選其中一literal為true(可能有很多個都是true,但我們就挑一個就好)
假設l4為true且共有7個literal,那麼經過改裝,加入新變數λi,其中λ1=true,其他依照規定加入,可得
(l1 ∨ l2 ∨ true)∧
(false ∨ l3 ∨ true)∧
(false ∨ l4 ∨ false)∧
(true ∨ l5 ∨ false)∧
(true ∨ l6 ∨ l7)
經過這樣可知,若CNF是satisfiable,3-CNF也會是satisfiable。
3-CNF-SAT → CNF-SAT
- 假設3-CNF是satisfiable
- 要證明不論λi是如何設定的,都可以使得CNF中的每個C都是true(至少C中有一literal為true),也就是3-CNF中至少有一literal為true。
用反證法證明,假設所有literal都是false,那麼
- 第一個clause的λ1必須為true,因為(l1 ∨ l2 ∨ λ1)是true。
- 而第二個clause (¬λ1 ∨ l3 ∨ λ2)也必須是true,所以λ2也必須是true。
- 根據這樣的規律,所有λi都必須是true。i=1~ n-3
- 那麼最後一個clause (¬λn-3 ∨ ln-1 ∨ ln)就會是false。和每一clause都必須為true這件是矛盾。
3-CNF-SAT ≤ Clique
欲得到:若F為satisfiable ⇔ G有size≥k的clique。
改裝3-CNF為圖論
- 有一3-CNF F = (x ∨ ¬y ∨ ¬z)∧ (¬x ∨ y ∨ ¬z)∧ (¬x ∨ ¬y ∨ z),共n(=3)個變數(literal = 9)。
- 用literal建立一圖G含有3n(=9)個nodes。
- 所有Nodes互相相連,除了(1)同一clause(2)和自己矛盾的(例如x和¬x)。
- 建立這樣的圖需花費O(n^2)。
讓兩問題的Instance互相對映
3-CNF-SAT → Clique
- 假設F為true,那麼每一clause C都會為true。
- 每個clause中至少有一literal為true,且不會互相矛盾。
- 這些為true的變數在G中會互相相連形成大小為k(=3)的clique。
Clique → 3-CNF-SAT
- 假設G有一clique C。其中
- 不會有兩nodes在同一clause。
- 根據建立G的方式,每個clause有一node在Clique C。
- 令每一個Clique C當中的node為true,使得每一clause皆為true。
Clique ≤p Vertex Cover
欲得到:G有size≥k的clique ⇔ 有size ≦ n-k 的Vertex Cover。
讓兩問題的Instance互相對映
Clique → Vertex Cover
考慮一圖G當中的互補圖 G'。(the graph complement G' of G)
若C是G當中的一clique,那麼在G'當中必定沒有C的點相連形成的邊。
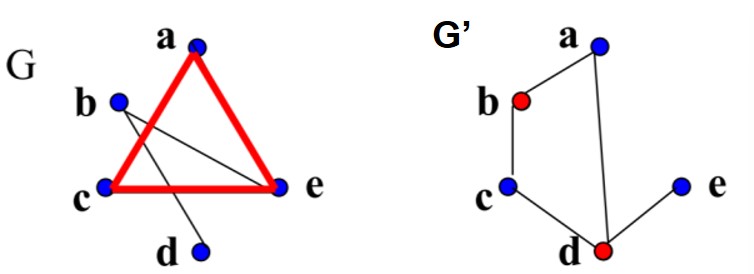
上面敘述代表,若G'當中有C中的點所連的邊,那麼其中一端點一定會落在V\C(V差集C),也就是說那V\C就可以覆蓋所有的邊,Vertex Cover。
Vertex Cover → Clique
- 考慮一圖G當中的互補圖 G'。(the graph complement G' of G)
- 假設D是G'當中的vertex cover,那麼D當中的nodes就會覆蓋G'的所有邊。
- 而V\D在G'就不相連,也就代表這些點在G當中會形成clique。
Vertex Cover ≤p Dominating Set
k-size vertex cover in G ⇔ k-size dominating set in G'。
改裝圖G
將G改為G':對G中的任一條邊都加入一點、兩條邊。
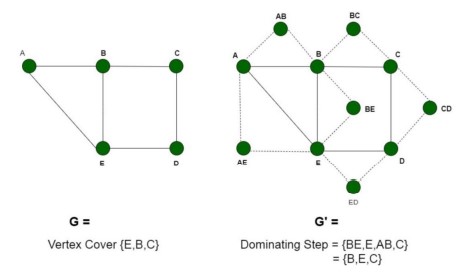
讓兩問題的Instance互相對映
Vertex Cover → Dominating Set
- 若C是G當中的vertex cover,代表C會覆蓋每一條邊。
- G'當中的每一條邊都是由原先C中的點所延伸出的,因此C在G'當中也可以蓋到每個點
Dominating Set → Vertex Cover
- 若D是G'當中的Dominating set,且不包含G'相較於G多加入的點。
- 因為D可以cover G'中的所有點,代表D也可以cover G中的所有邊。
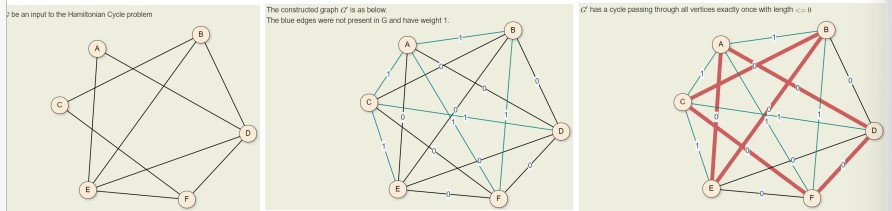
HC ≤p TSP
假設已知HC是NP-complete。再複習一次HC和TSP定義:
- HC:給予一undirected graph,找一cycle可經歷所有的點。
- TSP:給予一weighted complete graph和一臨界值L,找一cycley在cost ≤ L之下經歷所有的點
將本來HC當中的邊weight設為0,將本來兩點間沒有邊的地方加上邊,且新增加的邊weight設為1,則 有HC代表有≤0的TSP。